FCG-Chapter-4
4. 光线追踪
渲染是一个将输入对象进行处理、变成输出像素数组的过程。
有两种渲染方式:
- “object-order rendering”:每个对象依次被处理,所有被该对象影响的像素将会被查找并更新。
- “image-order randering”:每个像素依次被处理,所有影响到该像素的对象将会被找到并计算。
这两种方式都可以精确地获得完全相同的图像,但其计算的效果与性能十分不同。宽泛地来说,image-order rendering方式更容易跑起来,在可实现的视觉效果上也更灵活,并且在生成一张差不多的图像上经常(并非总是)占用更多的执行时间。
光线追踪是一种渲染3D场景的"image-order"算法,我们首先考虑它是因为,可以不用开发任何"object-order"渲染所需的数学工具。
4.1 基础光线追踪算法
光线追踪器的三个部分:
- 射线生成:计算每个像素基于相机几何的视射线的原点与方向。
- 射线求交:找到视射线的最近相交物体。
- 着色:基于射线相交结果,计算像素颜色。
基础光线追踪程序结构:
for each pixel do
compute viewing ray
find first object hit by ray and its surface normal n
set pixel color to value computed from hit point, lights, and n
4.2 透视
将3D物体/场景展示在一个2D图片上,有许多不同的方式:
线性透视(Linear Perspective):场景中的直线在图片中仍是直线。
平行透视(Parallel Projection):3D点将被移动到其2D投影位置上。
平行透视中有两种情况:当投影平面与视方向垂直时,这种投影称为正交投影(Orthographic),否则称为斜投影(Oblique)
平行透视常被用于机械、建筑制图中,因为它使3D场景中的平行线投影后仍然平行,且能保证与投影平面平行的物体尺寸不变。
但其缺点是未遵循人眼直觉中的“近大远小”,使得平行线“看起来不平行”。
**透视投影(Perspective Projection)**是一种计算透视的数学方法,它可以产生符合人眼直觉的图像。
4.3 计算视射线
从人眼\(e\)出发、经过一点\(s\)的射线可由下式表示:
$$\textbf{p}(t)=\textbf{e}+t(\textbf{s}-\textbf{e})$$一个面向对象的程序中,我们可能会这样表示:
class Ray
Vect3 o | ray origin
Vect3 d | ray direction
Vect3 evaluate(real t)
return o + t*d
相机坐标系:\(\textbf{e}\)作为原点,视线方向为\(-\textbf{w}\),“上方”向量(up vector)为\(\textbf{v}\),可构造右手坐标系的三个基向量\(\textbf{u},\textbf{v},\textbf{w}\)。
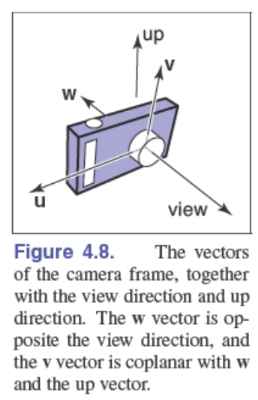
相机坐标系
4.3.1 正交视图
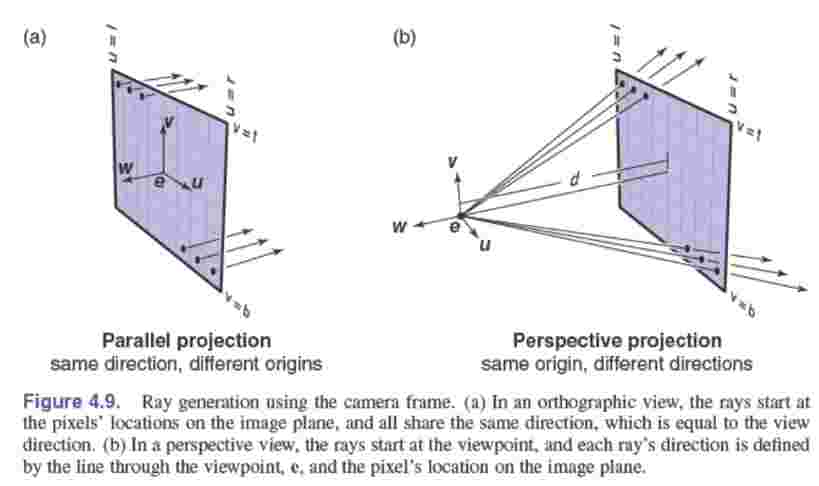
在正交视图中,所有射线都朝向\(-\textbf{w}\)。尽管平行视图中不存在视点(Viewpoint),我们仍然可以使用相机坐标系。
图像位置由四个参数定义:l,r,b,t 分别表示图像左边线、右边线的坐标位置(\(\textbf{u}\)坐标分量),下边线、上边线的坐标位置(\(\textbf{v}\)坐标分量)。
通常 \(l < 0 < r\) 且 \(b < 0 < t \) 。
相机坐标系
在相机坐标系下,图片像素\((i,j)\)的坐标可按下式计算:
$$u=l+(r-l)(i+0.5)/n_x$$$$v=b+(t-b)(j+0.5)/n_y$$在正交视图中,可以把图片像素位置当做射线原点,正交视图下的射线生成如下:
compute u and v of a pixel
ray.\(\textbf{o}\) ← \(\textbf{e}\) + u\(\textbf{u}\)+v\(\textbf{v}\)
ray.\(\textbf{d}\) ← -\(\textbf{w}\)
(译注:按个人理解,\(e\)的绝对位置不重要,只要保证它不穿越到图片另一侧。射线起点在每个像素位置上)
要实现斜平行视图,只需要将图片平面法向\(\textbf{w}\)与射线方向\(\textbf{d}\)分开处理即可。
4.3.2 透视视图
图片平面距离/焦距(Image Plane Distance):视点到图片平面的距离。
射线计算过程:
compute u and v of a pixel
ray.\(\textbf{o}\) ← \(\textbf{e}\)
ray.\(\textbf{d}\) ← -d\(\textbf{w}\) + u\(\textbf{u}\)+v\(\textbf{v}\)
和平行投影一样,斜透视视图可以通过将图片法向与投影方向分开处理来实现。
(译注:在什么情况下会使用斜透视?)
4.4 射线-物体求交
4.4.1 射线与球相交
给定一条射线 \(\textbf{p}(t)=\textbf{e}+t\textbf{d}\) 以及一个隐式表面 \(f(\textbf{p})=0\),其交点的t值可用如下方程计算:
$$f(\textbf{p}(t))=0 \quad or \quad f(\textbf{e}+t\textbf{d})=0$$球心为 \(\textbf{c}=(x_c,y_c,z_c)\)、半径为\(R\)的球面方程为:
$$(x-x_c)^2+(y-y_c)^2+(z-z_c)^2-R^2=0$$或者以向量表示:
$$(\textbf{p}-\textbf{c})\cdot(\textbf{p}-\textbf{c})-R^2=0$$$$\Rightarrow(\textbf{e}+t\textbf{d}-\textbf{c})\cdot(\textbf{e}+t\textbf{d}-\textbf{c})-R^2=0$$$$\Rightarrow(\textbf{d}\cdot\textbf{d})t^2+2\textbf{d}\cdot(\textbf{e}-\textbf{c})t+(\textbf{e}-\textbf{c})\cdot(\textbf{e}-\textbf{c})-R^2=0$$这是一个二次方程,其解为:
$$t=\frac{-\textbf{d}\cdot(\textbf{e}-\textbf{c})\pm\sqrt{(\textbf{d}\cdot(\textbf{e}-\textbf{c}))^2-(\textbf{d}\cdot\textbf{d})((\textbf{e}-\textbf{c})\cdot(\textbf{e}-\textbf{c})-R^2)}}{(\textbf{d}\cdot\textbf{d})}$$在实际实现中,你应该首先检查其判别式(discriminant),以确定有几个解。
交点\(\textbf{p}\)上的法向量可以通过梯度计算:
$$\textbf{n}=2(\textbf{p}-\textbf{c})$$其单位法向量为:
$$(\textbf{p}-\textbf{c})/R$$4.4.2 射线与三角形相交
射线与参数曲面相交,其笛卡尔坐标满足:
$$\left. \begin{matrix} x_e+tx_d=f(u,v)\\ y_e+ty_d=g(u,v)\\ z_e+tz_d=h(u,v) \end{matrix} \right\}\quad \mathrm{or,} \quad \textbf{e}+t\textbf{d}=\textbf{f}(u,v)$$在本节中三角形顶点为\(a\),\(b\)和\(c\)一个参数平面,使用 2.9.2节 的向量形式表示,则交点满足:
$$\textbf{e}+t\textbf{d}=\textbf{a}+\beta(\textbf{b}-\textbf{a})+\gamma(\textbf{c}-\textbf{a})$$当且仅当\(\beta>0\),\(\gamma>0\)且\(\beta+\gamma<1\)时交点位于三角形内。