我什么也不做,并且睡得很晚
FCG-Chapter-2
这一章内容繁杂,暂时跳过
2. 混杂的数学知识
本章是数学知识大杂烩,仅作为参考而非严密教程。与“标准数学”的区别在于,本章着重于强调几何解释。建议读者跳过熟悉的内容,在需要时再返回来参阅。
2.1 集合与映射
2.1.1 逆映射
2.1.2 区间
2.1.3 对数
2.2 求解二次方程
2.3 三角学
2.3.1 角
2.3.2 三角函数
2.3.3 实用恒等式
2.3.4 立体角与球面三角学
2.4 向量
2.4.1 向量运算
2.4.2 向量的笛卡尔坐标
2.4.3 点积
2.4.4 叉积
2.4.5 标准正交基与标架
2.4.6 从单个向量构造基
2.4.7 从两个向量构造基
2.4.8 正交化基
2.5 积分
2.5.1 均值与带权均值
2.5.2 在立体角上的积分
2.6 密度函数
2.7 曲线与曲面
2.7.1 二维隐式曲线
2.7.2 二维梯度
2.7.3 三维隐式曲面
2.7.4 隐式曲面的表面法向量
2.7.5 隐式平面
2.7.6 二维参数曲线
2.7.7 三维参数曲线
2.7.8 三维参数曲面
2.7.9 曲线、曲面总结
2.8 线性插值
2.9 三角形
平面以及空间三角形是许多图形程序中的基本建模图元,通常像颜色之类的信息都是被附加在三角形顶点之上的,在整个三角形上进行插值。
有一种坐标表示法可以让这个插值变得简单、直接,它就是重心坐标。
2.9.1 平面三角形
对于一个顶点为\(a\),\(b\),\(c\)的平面三角形,它的有向面积为:
$$ Area = \frac{1}{2} \begin{vmatrix} x_b - x_a & x_c - x_a \\ y_b - y_a & y_c - y_a \end{vmatrix} $$当\(a\),\(b\),\(c\)为逆时针排列时,该面积为正值,否则为负值。
重心坐标是一种非正交的坐标系,如下图所示,这样的坐标系以\(a\)为原点,\(a\)到\(b\)和\(c\)的向量为基向量。
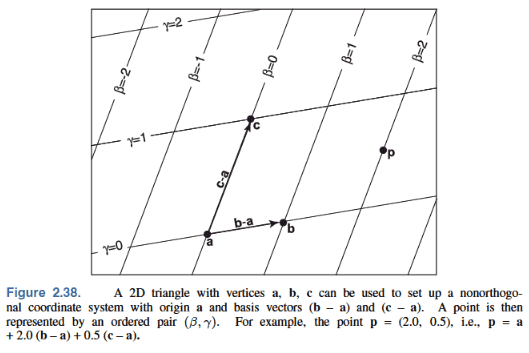
重心坐标系
这样平面上任意一点\(\textbf{p}\)可以表示为:
$$ \textbf{p} = \textbf{a} + \beta (\textbf{b} - \textbf{a}) + \gamma (\textbf{c} - \textbf{a}) $$重新整理一下上式:
$$ \textbf{p} = (1-\beta-\gamma) \textbf{a} + \beta \textbf{b} + \gamma \textbf{c} $$为了对称性,可定义变量\(\alpha\):
$$ \alpha = 1 - \beta - \gamma $$得到如下方程:
$$ \textbf{p}(\alpha, \beta, \gamma) = \alpha \textbf{a} + \beta \textbf{b} + \gamma \textbf{c} $$$$ \alpha + \beta + \gamma = 1 $$该坐标表示有一个很好的特点,当\(\textbf{p}\)在以\(a\),\(b\),\(c\)为顶点的三角形内部时,当且仅当:
$$ 0 < \alpha < 1 $$$$ 0 < \beta < 1 $$$$ 0 < \gamma < 1 $$给定任意点\(\textbf{p}\),求解如下方程可得其重心坐标:
$$\left\{\begin{matrix} \begin{bmatrix} x_b - x_a & x_c - x_a \\ y_b - y_a & y_c - y_a \end{bmatrix} \begin{bmatrix} \beta \\ \gamma \end{bmatrix} \begin{bmatrix} x_p - x_a \\ y_p - y_a \end{bmatrix} \\ \alpha = 1 - \beta - \gamma \end{matrix}\right.$$在几何上,\(\textbf{p}\)的重心坐标与其与三边组成三角形的有向面积有关:
$$ \alpha = A_a / A $$$$ \beta = A_b / A $$$$ \gamma = A_c / A $$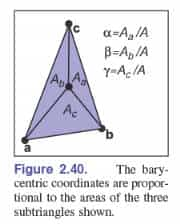
有向面积计算重心坐标
2.9.2 空间三角形
重心坐标也可扩展到三维情形,假设有三个空间点\(a\),\(b\),\(c\),可以这样表示:
$$ \textbf{p} = (1-\beta-\gamma)\textbf{a} + \beta \textbf{b} + \gamma \textbf{c} $$通过改变\(\beta\)和\(\gamma\),可以扫掠整个平面。
三角面的法向量可以用两条边向量的叉积计算:
$$ \textbf{n} = (\textbf{b} - \textbf{a}) \times (\textbf{c} - \textbf{a}) $$三角形面积:
$$ area = \frac{1}{2} || (\textbf{b} - \textbf{a}) \times (\textbf{c} - \textbf{a}) || $$注意,这个公式计算得到的不是有向面积。
但我们仍然可以通过判断子三角形与主三角形的法向量符号关系来判断其有向面积符号,从而计算空间三角形的重心坐标:
$$ \alpha = \frac{\textbf{n} \cdot \textbf{n}_a}{||\textbf{n}||^2} $$$$ \beta = \frac{\textbf{n} \cdot \textbf{n}_b}{||\textbf{n}||^2} $$$$ \gamma = \frac{\textbf{n} \cdot \textbf{n}_c}{||\textbf{n}||^2} $$其中:
$$ \textbf{n}_a = (\textbf{c} - \textbf{b}) \times (\textbf{p} - \textbf{b}) $$$$ \textbf{n}_b = (\textbf{a} - \textbf{c}) \times (\textbf{p} - \textbf{c}) $$$$ \textbf{n}_c = (\textbf{b} - \textbf{a}) \times (\textbf{p} - \textbf{a}) $$